
本周推荐的几篇文章都和平均值(Mean)有关。
人们在分析问题和定义指标时经常使用平均值,因为平均值可以把现实世界中复杂的行为压缩为一个数字,进行理解和相互比较。
在实际应用中,只看平均值往往是非常危险的,因为平均数可能受到极少样本的影响,比如某大厂员工平均月薪七万也可能是算上首富以后的平均结果。
以下是本周的推荐。
1. Basketball Analytics, Part 2: Shot Quality
本文的副标题是 Yes 3’s are better than long 2’s, but that’s not the whole story。作者给出了一组 NBA 球队得分手段效率之间的对比数据,选取的衡量指标是平均每次投球得分(points per shot) 。
其中上篮和灌篮的平均 pps 最高,但随着投球点远离篮筐,pps 开始下降,因为命中率降低了,但三分球的 pps 又比所有中投的 pps 都要高。也就是说假如所有球队在每场篮球比赛中都能获得 100 次出手机会,只投三分球的球队将会比只投两分球的球队多得 26 分。

只考虑平均的 pps 是不够的,因为一种可能的解释是,三分球效率之所以那么高,很可能是被少数几名三分球神射手拉起来的。因此,作者补充了一份数据: 2021 赛季有多少名球员在中距离出手上比三分球效率更高?
The next step we might take to examine this question is to see if there are some players who buck the trend. In statistics, we like to aggregate things together and take averages. But we can benefit from getting more precise. After all, there are some players that we consider to be midrange specialists. So let’s see if these players tend to be more efficient from the midrange than from 3.
在观察的 274 名球员中,只有 21 人的中距离投篮效率更高,不到所有玩家的 8%,其他所有球员的三分球效率都高于中距离,其中不乏 Chris Paul 和 Kawhi Leonard 这样的顶级中投手。
根据以上两项观察,一种潜在的推论是 NBA 球队应该减少中距离跳投,而增加上篮和三分球出手。例如 Joe Harris 场均出手 6.4 次,三分命中率高达 47%,全联盟第一,有人可能会说:「网队应该让他只投三分球。」 但任何一个篮球迷都能凭直觉告诉你这是天方夜谭。
Joe Harris 三分球效率如此之高的原因之一是他选择了那些更好的时机来投球,在不改变球队战术的前提下,Joe Harris 增加他三分球出手次数的唯一办法就是在那些相对来讲没那么好的时机也出手,这反过来又会降低他的得分效率。
2. How Much Should You Bet To Maximize Your Investments, or Your Company's Odds of Success?
这篇文章来自红点风险投资人 Tomasz Tunguz,是我非常喜欢的一个 blogger。在这篇文章中,他介绍了著名的凯利公式,一个由 John Kelly 从香农信息论发展出来的财富公式。
凯利公式用于回答投资上的基本问题:如果我给你 1000 元用于投资,有 5 个投资方案,你应当如何决定?如果你是一家创业公司的 CEO,一家 VC 投了你 1000 万美金,你的 VP 们有 5 个不同的项目想法,你会怎么做选择?凯利公式有两个很关键的想法,一是要避免资产归零,二是要尽快实现增长。
首先,计算投资的期望价值时应该使用几何平均( geometric mean),而非普通的算术平均,算术平均 (arithmetic mean ) 就是我们平日里更加熟悉的那个「平均」——average。
如果你有三个投资选项,每个选项的胜率都一样,但它们的回报率分别为 100%、50% 和0%。那么,回报率的算术平均为 50%,但几何平均是 0%,凯利公式就说不要投资。因为几何平均考虑了复利,算术平均没有。事实上,所有增长场景下的比例计算,都应该使用几何平均来求平均。
.
其次,投资的规模由风险和回报共同决定,凯利公式说,项目回报(edge)越高,胜率越高,投资占总资产的比例就应该越大。
How do you calculate how much to bet? Kelly criterion says to bet more the greater your edge and the likelihood of success.
下面这个公式中,KC 是投资占总资产的比例,W 是胜率,R 是赔率。如果胜率是 100%,没有理由不选择 all-in 筹码。
KC = W - (1-W)/R
除了投资人以外,很多赌徒也迷恋这个公式。它在德州扑克中的一个应用就是,在某一轮决定是否要跟注时,只需要看跟注后的胜率是否超过了底池的赔率。
3. Analysis of “What’s 2/3 of the Average”
平均数是反映数据集中性趋势(central tendency)的测量。本文讲了一个著名的博弈论游戏,一群人每人挑选 0 到 100 之间的一个数字,最接近平均值 2/3 的人将获得游戏胜利。
这道题的第一层是假设每个人都随机做选择,那么平均数的最大值也不可能超过 67,因此可以认为存在这样的共识:所有人都不会选 67 以上的数字,于是有效的选择范围变成了 0 到 66。
那么,假设每个人在 0 到 66 之间随机做选择,同样没有人想选择大于 44 的数字,因为 0 到 66 之间随机数字平均值的 2/3 不可能超过 44,而一旦选择了 44 以上的数字就不可能获胜,而大家都是理性的……
于是这道题就变成了一个「其他人也都是理性的」递归推理,丹麦新闻曾经对 2 万人规模的群体进行实验最终结果是 21.6,这个结果一定程度上表明了绝对理性的共识在现实情况中不会发生。
4. Beware the mean
人们在定义 KPI 时往往会使用平均值,因为平均值可以将现实世界中的复杂行为压缩为一个数字,牺牲精确来换取清晰在很多情况中是有效的,也是可取的。
但 Stephen Whitworth 指出我们应该警惕平均,尤其对于那些幂律分布的指标(例如成本、收入、参与度),研究前 1% 用户的行为比看它们的平均值更加有意义,原文用了迷人一词。
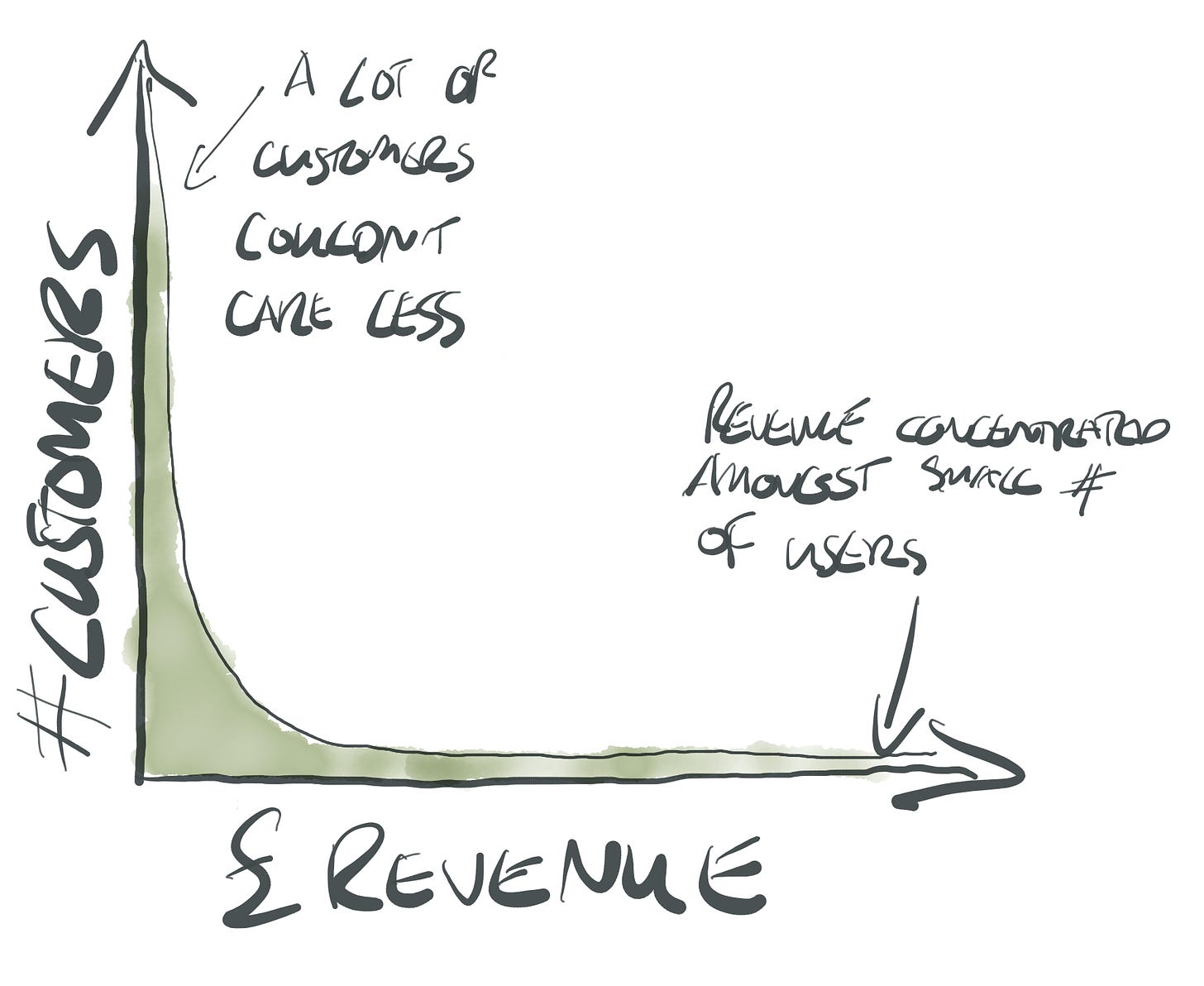
典型的例子是 Slack ,1% 的客户贡献了 40% 的收入。
Whitworth 鼓励人们设置 KPI 和目标时,避免将所有指标简化为一个数字,并只提高单个数字,因为这种简化会忽略掉很多重要信息。而应该关注指标的分布,并尝试把这个分布变成一个你想要的形状,为此可以引入中位数和百分位数这样的统计量,例如:
The median customer must be profitable.
The 90th percentile customer must make us £x, the 99th percentile should make us £Y, and the maximum at least £Z.
以上是本期的推荐,希望对你有用。
我在上一期中推荐了数据团队的《凤凰项目》,后来我翻译了全文,感兴趣的朋友可以通过这个链接一口气看完。
Dreamsome
下周见!
❤️ 想支持《数据科学人》?把它推荐给 3 个朋友吧!
🚀 欢迎用电邮订阅《数据科学人》,我将以周报的形式发布内容